どうも、ぽんせいです!
皆さんはボロノイテクスチャを使っていますか?
そもそもボロノイってなんでしょうか?なんか色々模様が出ますよね。
使っている人も、その効果などをよく理解しないまま使っていると思います。
この記事では、ボロノイテクスチャについて、徹底的に解説していきます。
ボロノイテクスチャとは?
ボロノイテクスチャとは、CGやコンピュータグラフィックスにおいて使用される、セル状のパターンが特徴的なテクスチャ手法です。蜂の巣や亀の甲羅、石の割れ目など、自然界によく見られる模様を再現するために使われます。
このテクスチャは、「ボロノイ図(Voronoi Diagram)」と呼ばれる数学的構造を基にしています。空間上の複数の点(シード)からの距離に基づき、領域を分割することで生成されるため、自然な不規則性を持ちながらも秩序を感じさせる模様になります。
![{\displaystyle V(p)=\{x\in X\mid \forall q\in P\;[d(x,p)\leq d(x,q)]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d1446f30d756fdcd9d18f63ac1e39ca64a5ab29)
を p の(ボロノイ)領域と呼び、P の全ての点の領域を集めた集合(の誘導するセル複体)をボロノイ図と呼ぶ。
意味不明ですね!
私もこんな数式見せられても全然わかんないです。
簡単にしてみましょう!
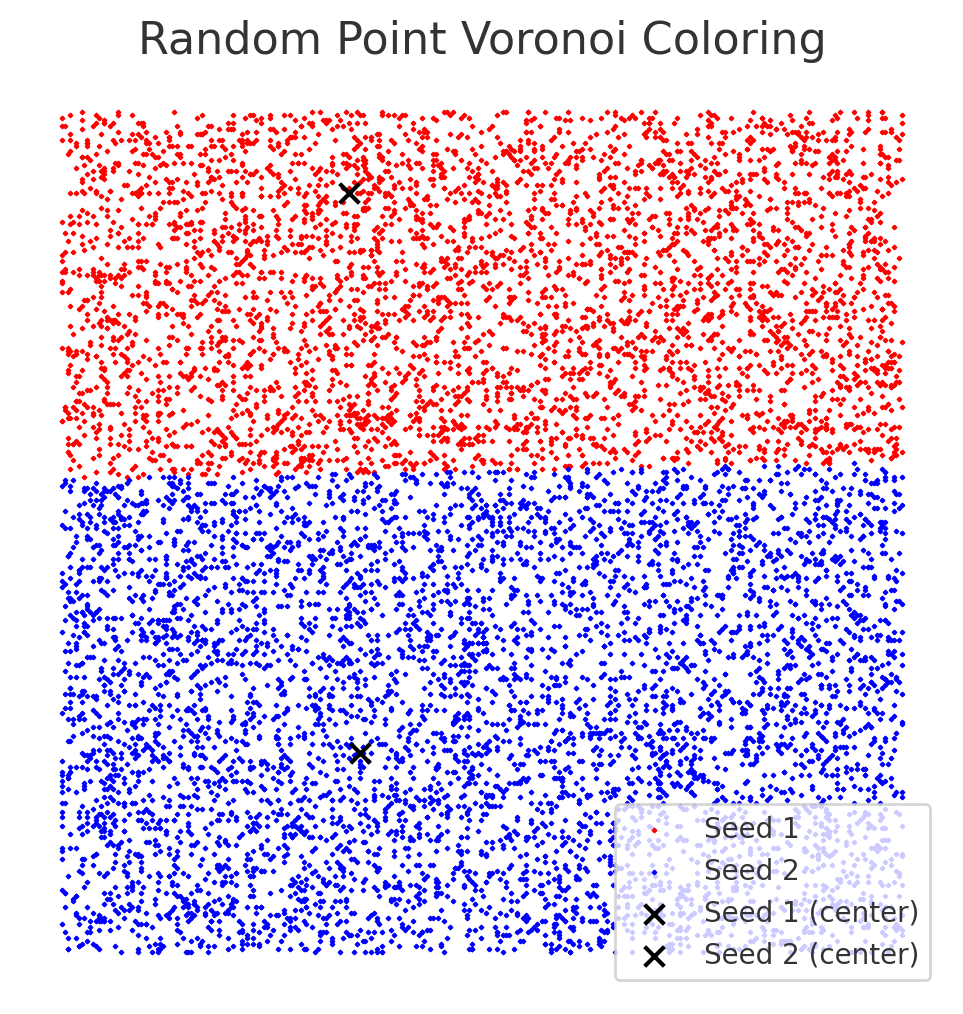
これは、点でできた図に2つの母点を置きます。この2つの母点のうち、上の母店に近い方を赤、下の母点に近い方を青に色付けしています。
これが、ボロノイテクスチャを簡単に表した図です。
では、この母点を5つに増やしてみましょう!
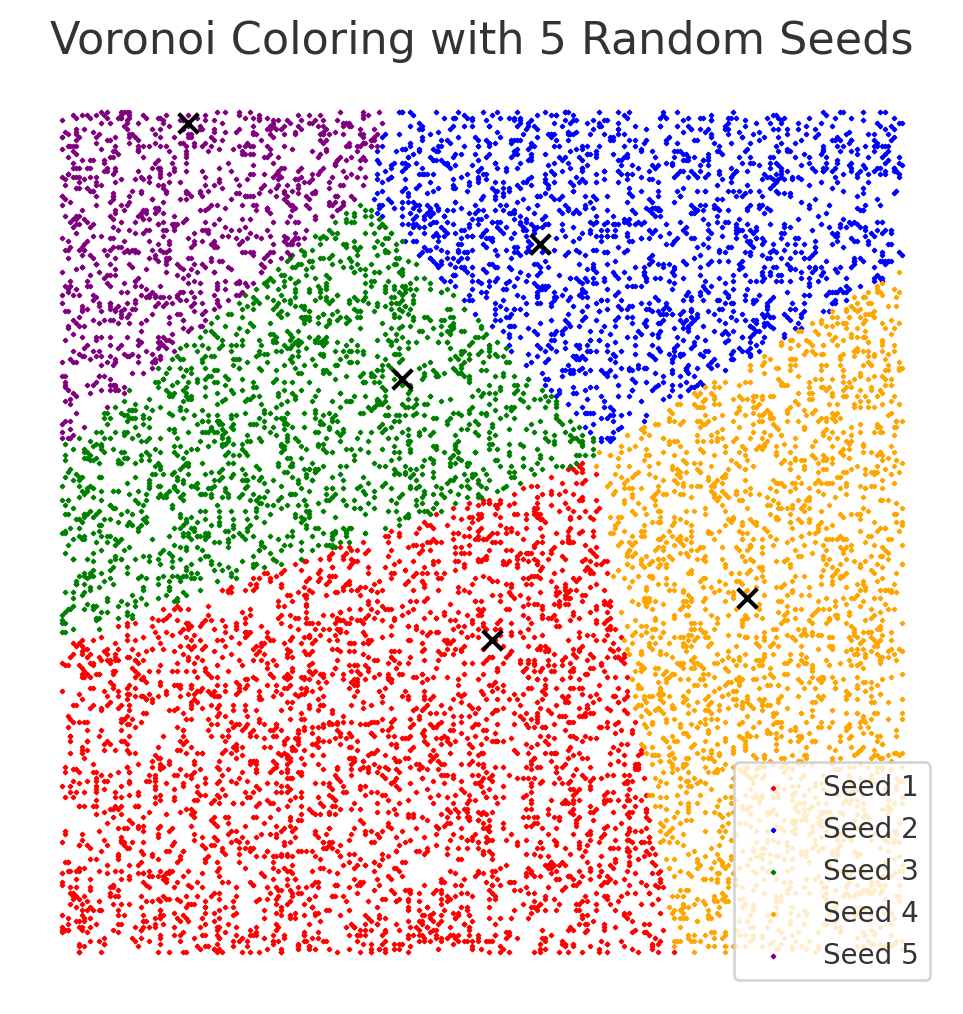
それっぽい図になりましたね!
この色ごとの境界線は、母点を結んだ線の垂直2等分線上にあります。
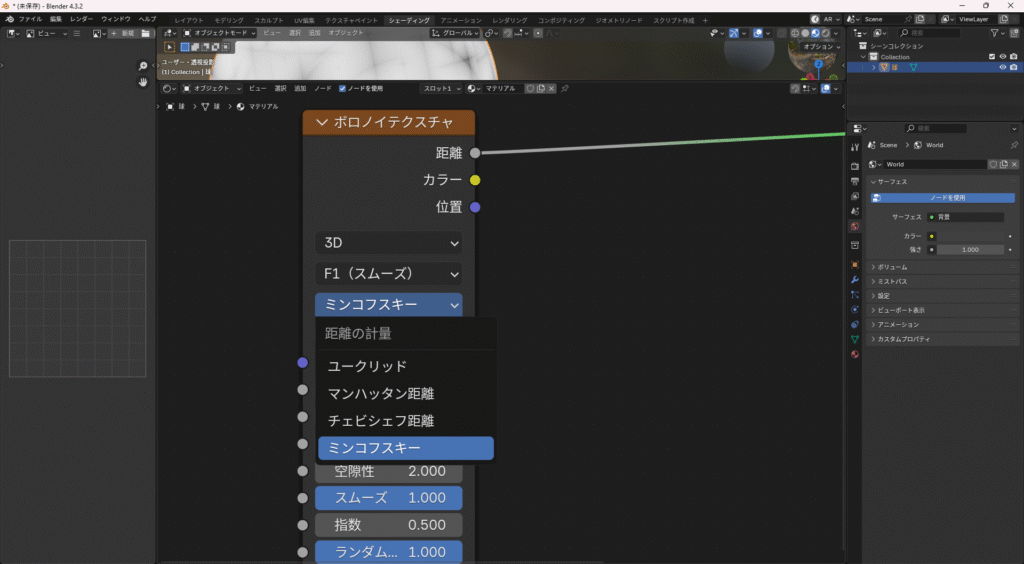
Blenderではこんな風にバリエーションがありますよね。
これらはそれぞれ何が違うんでしょうか?
ボロノイテクスチャの種類
ボロノイテクスチャには、使用する距離関数やセルの特性によってさまざまなバリエーションがあります。それぞれの方式は、模様の形状やニュアンスに大きな影響を与えます。
ユークリッド距離
これが一番スタンダードな形式です。
ユークリッド距離とは2点間の「直線距離(最短距離)」を表す距離のことです。
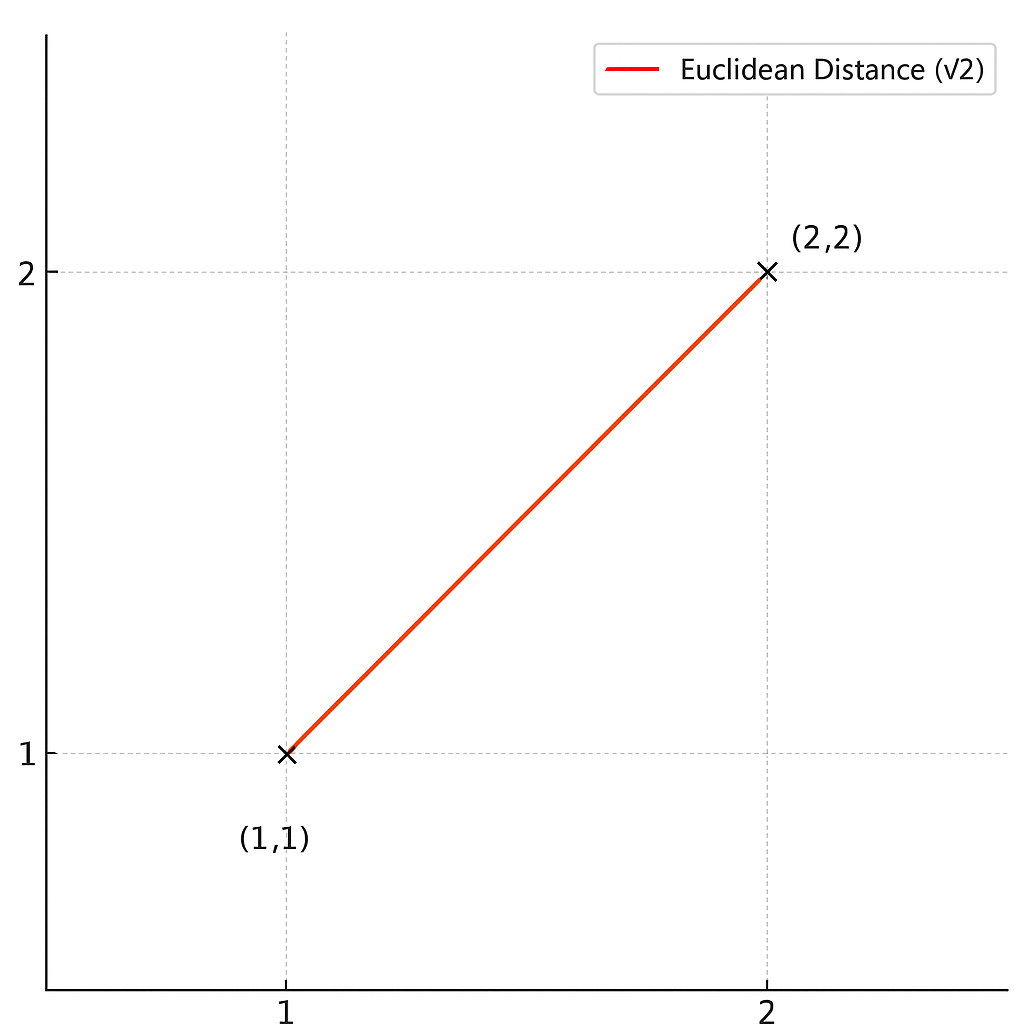
Blender で表すとこんな感じになります。
さっきの図と似ていますね。
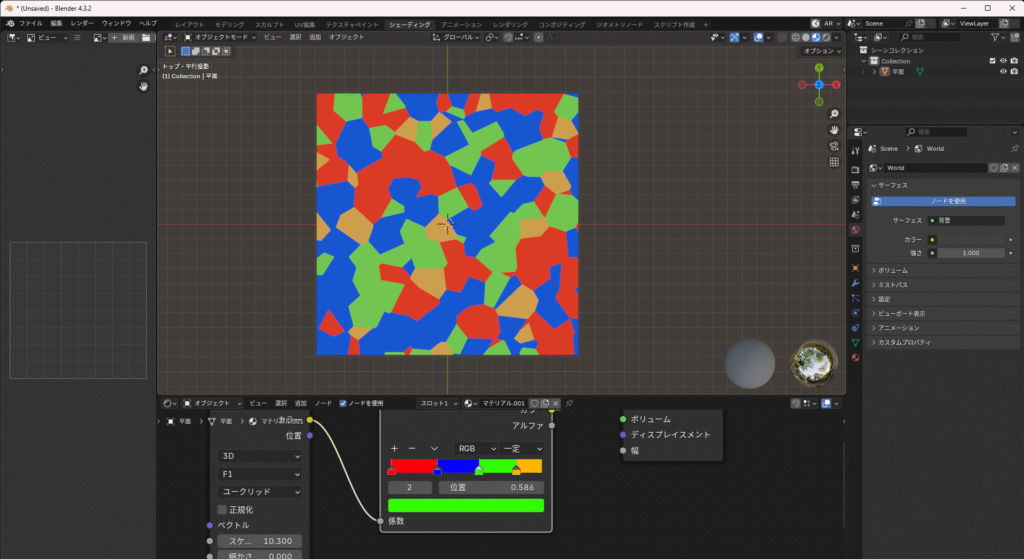
マンハッタン距離
各軸方向の移動距離の合計で定義されます。
つまり、斜めに移動できないということです。名前の由来になったマンハッタンの街は、碁盤の目状(グリッド状)に道路が整備されています。

・縦と横の通りしかない
・斜めに道を通れない
・ある交差点から別の交差点へ行くには、縦と横に曲がって移動する必要がある
つまり、「斜め移動ができない環境」ということです。
ユークリッド距離との違いはこんな感じです。
ユークリッド距離は縦、横、斜めの最短距離です。よって、√2となります。
一方マンハッタン距離は縦、横のみなので、2となります。
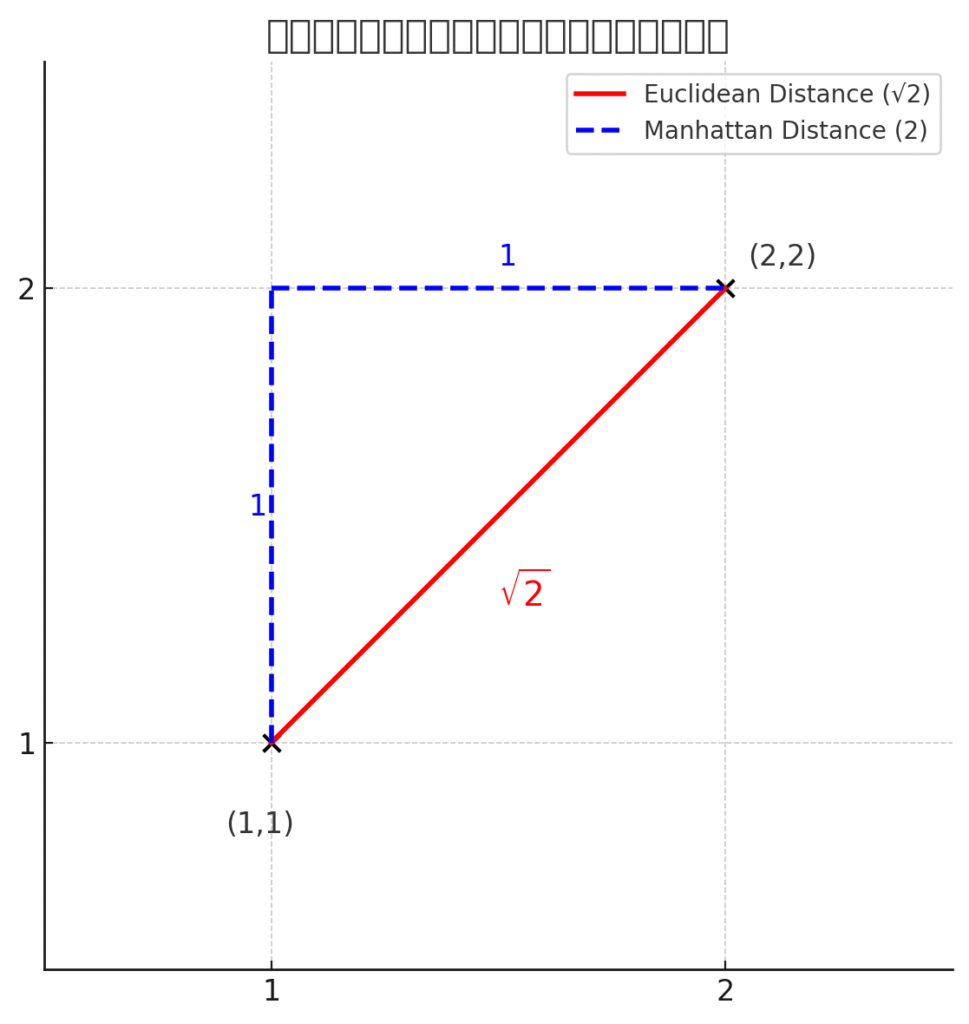
ユークリッド距離とマンハッタン距離の長さの違いはこんな感じになります。
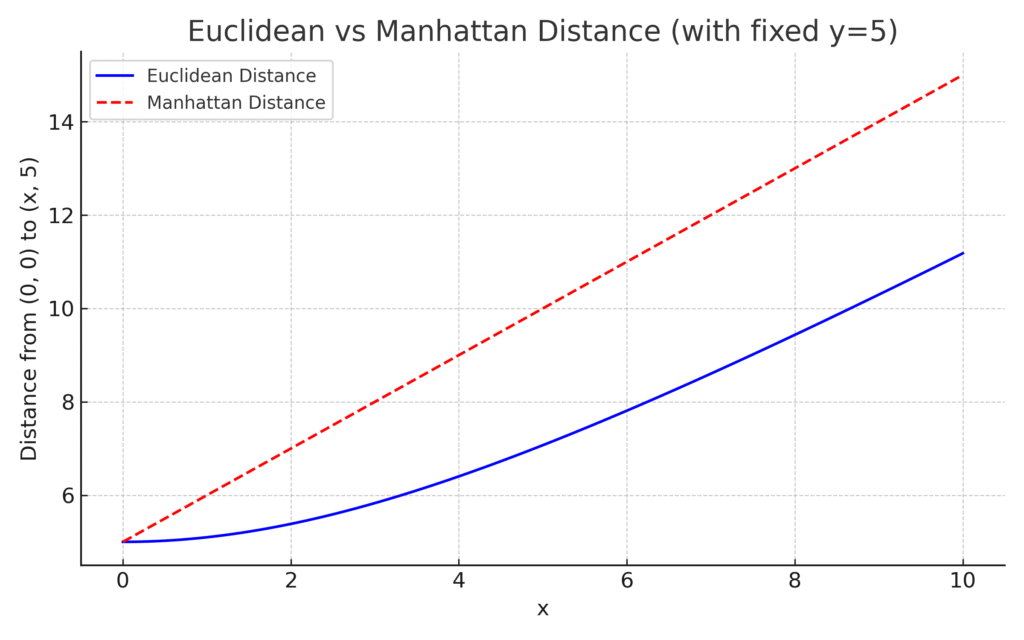
🟦青線:ユークリッド距離(曲線)
- 点 (0, 0) から (x, 5) までの直線距離
- 放物線的にゆるやかに増加します
🟥赤線:マンハッタン距離(直線)
- 点 (0, 0) から (x, 5) までの縦+横移動
- 一直線に増加
Blenderで表すとこんな感じになります。
直線的で角ばった領域分けになっており、形が直線的でブロックっぽいです。
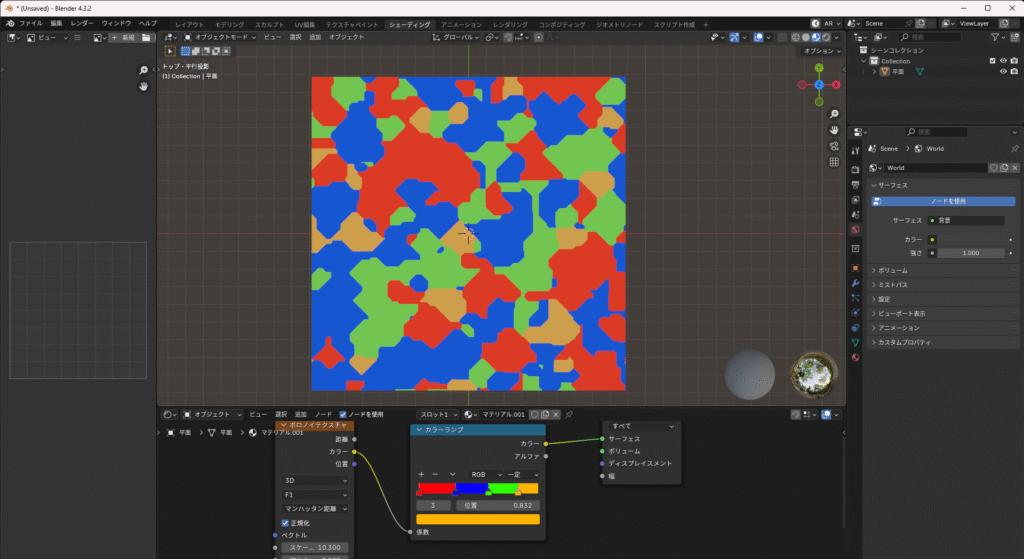
チェビシェフ距離
軸ごとの移動距離の最大値を使用します。
これは、グラフで表すとこんな感じです。
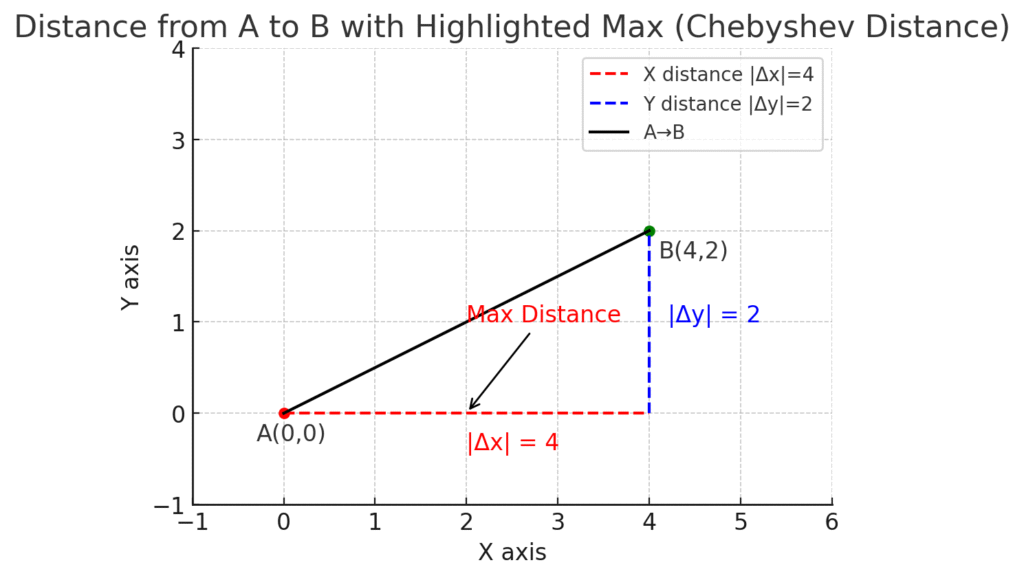
AからBまで移動します。
X軸上の移動距離の絶対値は4
Y軸上の移動距離の絶対値は2となります。
チェビシェフ距離とはこの絶対値の大きい方を取ったものです。今回は4になりますね。
Blenderで表すとこんな感じになります。
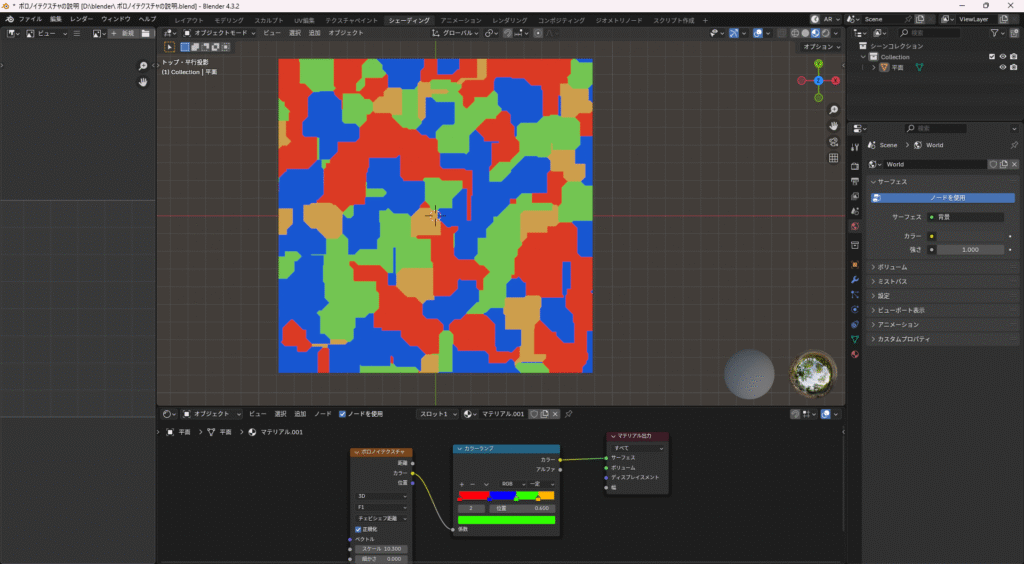
ミンコフスキー
このミンコフスキーは、数学とかにあるミンコフスキー距離とは少し違います。
数学のミンコフスキー距離とは、ユークリッド距離やマンハッタン距離、チェビシェフ距離をすべて含む「一般化された距離」の考え方です。
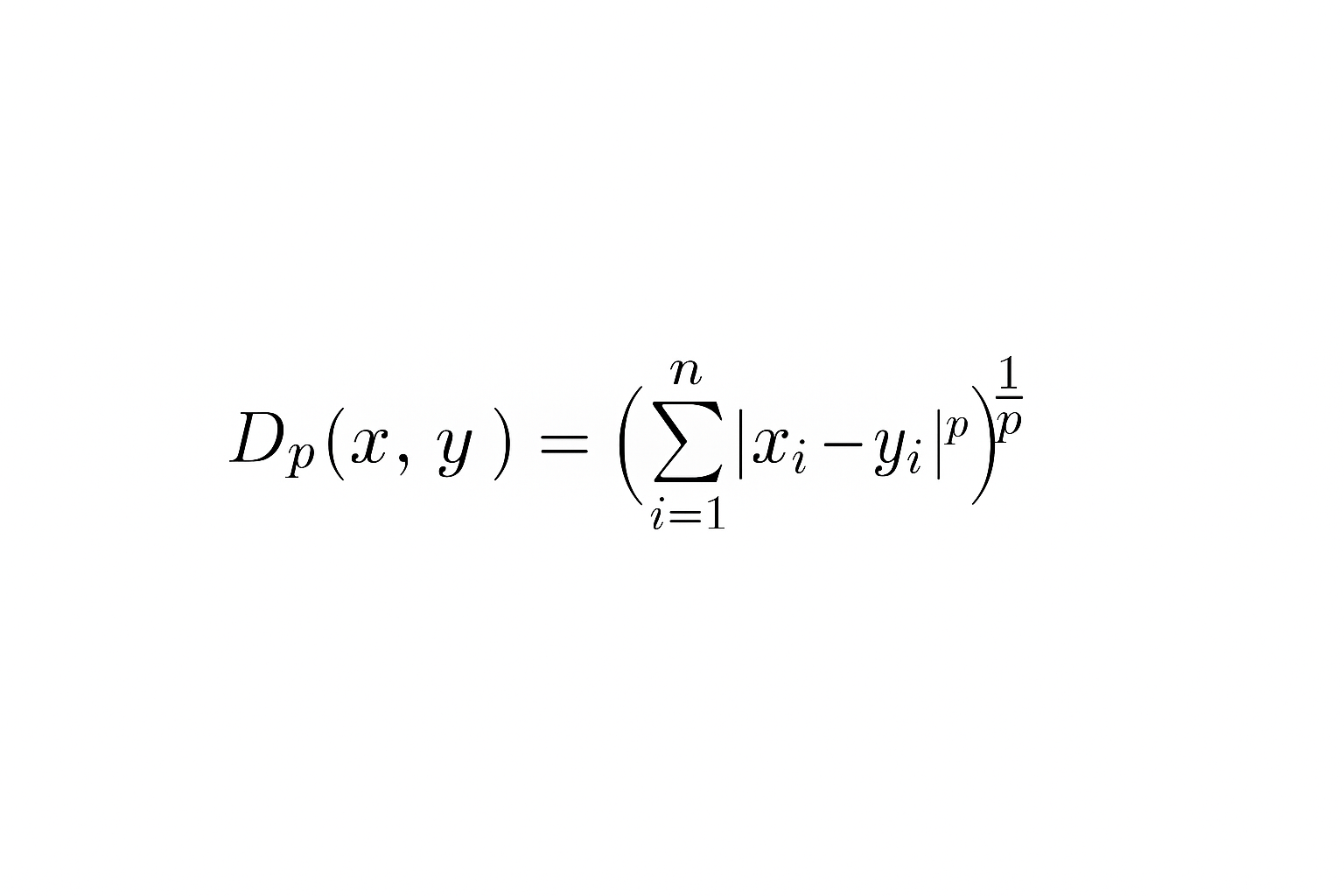
この公式のPを変えることで距離の種類が変わります。
| ppの値 | 距離の種類 | 特徴 |
|---|---|---|
| p=1p = 1 | マンハッタン距離 | 縦横だけで移動する距離 |
| p=2p = 2 | ユークリッド距離 | 直線距離(最短距離) |
| p→∞p \to \infty | チェビシェフ距離 | 各座標の差の最大値 |
BlenderのミンコフスキーはPの値などは無いため、p値が2〜∞の中間程度の距離が使われていると推測できます。
ユークリッド:完全な円形セル
マンハッタン:完全なひし形セル
チェビシェフ:完全な四角形セル
ミンコフスキー:これらの中間で柔らかな角を持つセル
こんな感じのイメージがいいと思います。
F1、F2とは?
ボロノイテクスチャには「F1」と「F2」というモードがあり、それぞれ模様の出方が変わります。
F1は、各ポイントから最も近いセルまでの距離を元に模様を作るため、よく見るひび割れや細胞のような模様になります。
一方、F2は2番目に近いセルまでの距離を元にしているので、F1よりも複雑でランダム感のある独特なパターンを作れます。
シンプルな模様が欲しいときはF1、より変化に富んだ質感を出したいときはF2を試すと良いでしょう。
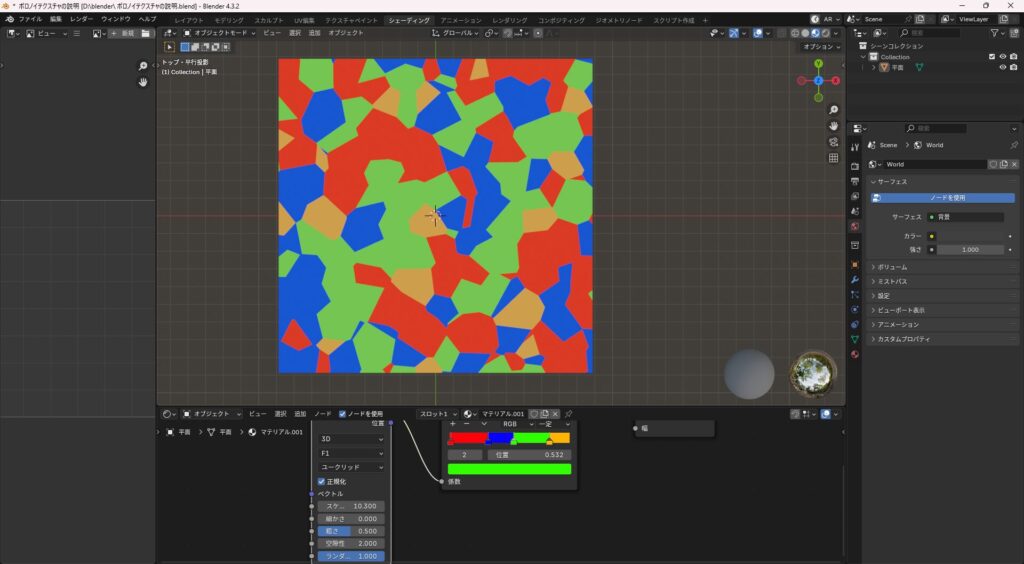
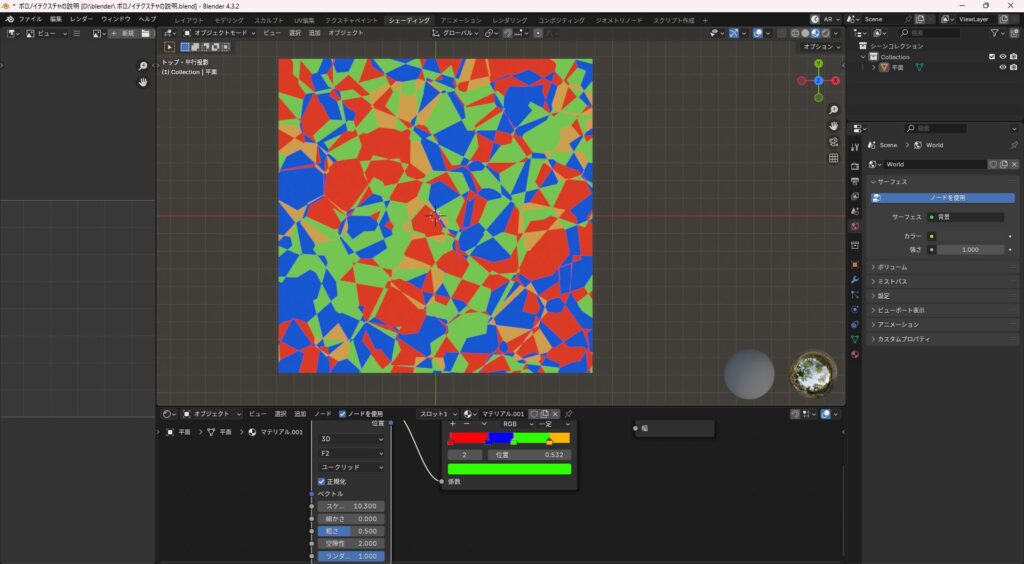
F1、F2でかなり見た目に変化が出ますね。
次元について
ボロノイテクスチャの次元とは、どの空間の中に模様を生成するかを決める設定です。簡単に言えば、「線」「平面」「立体」「時間変化」など、どのレベルで模様を計算するかを選ぶことができます。
設定できる次元は以下の4つ:
| 次元設定 | 説明 | 主な用途 |
|---|---|---|
| 1D | 1次元(線上での模様) | 実験的な表現、シンプルなパターン |
| 2D | 2次元(平面上の模様) | UVマッピングされた表面模様など |
| 3D | 3次元(立体的な模様) | 立体オブジェクト内部まで模様を入れたい時 |
| 4D | 4次元(時間変化を含む模様) | 動く模様、アニメーション素材 |
1D(1次元)
- 線の上に模様を配置
- 実用性はあまり高くない
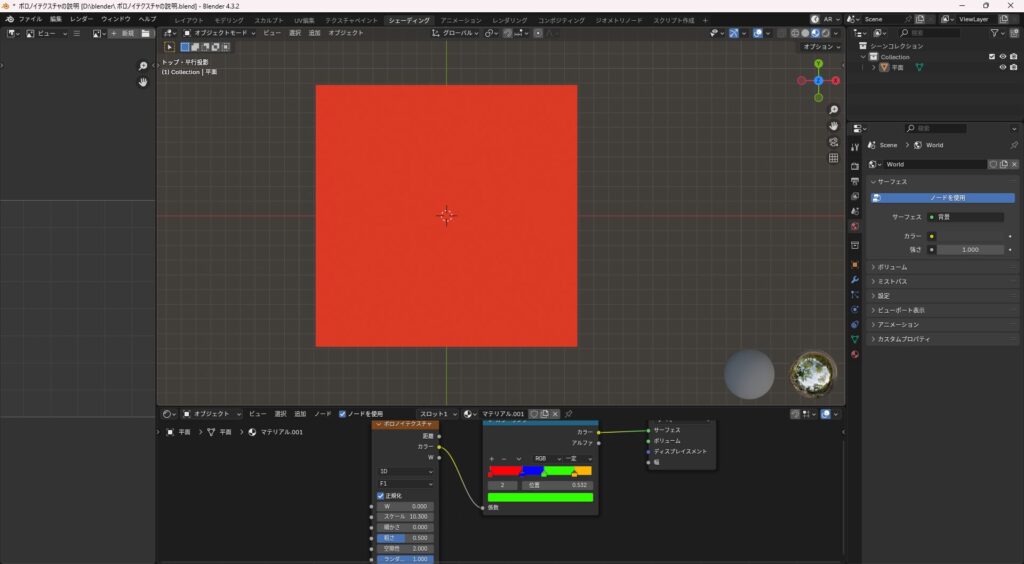
2D(2次元)
- X軸・Y軸の平面に模様を生成
- 一般的なテクスチャ、サーフェスの質感づくりに最適
- ひび割れ、タイル模様、細胞模様などが表現できる
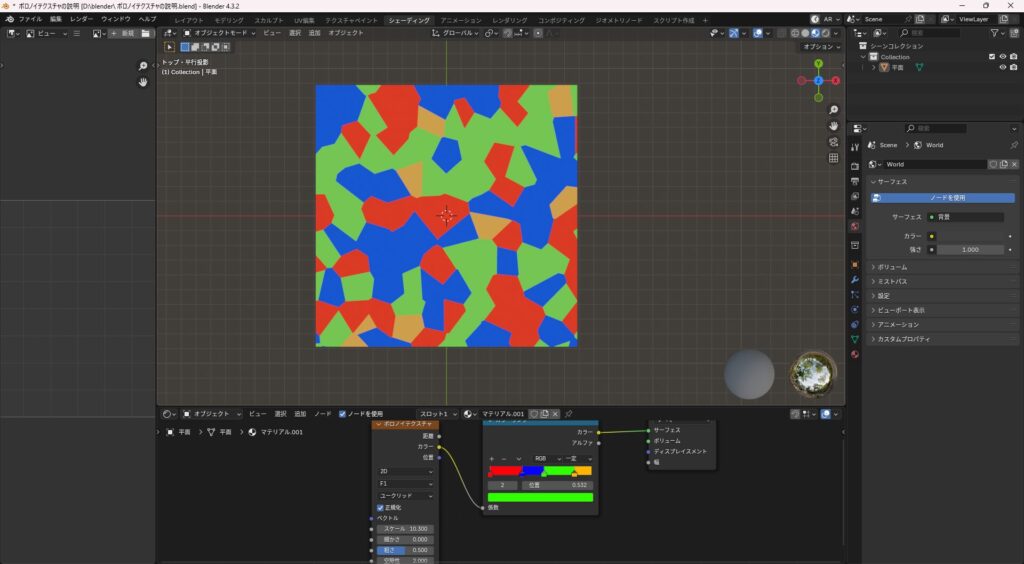
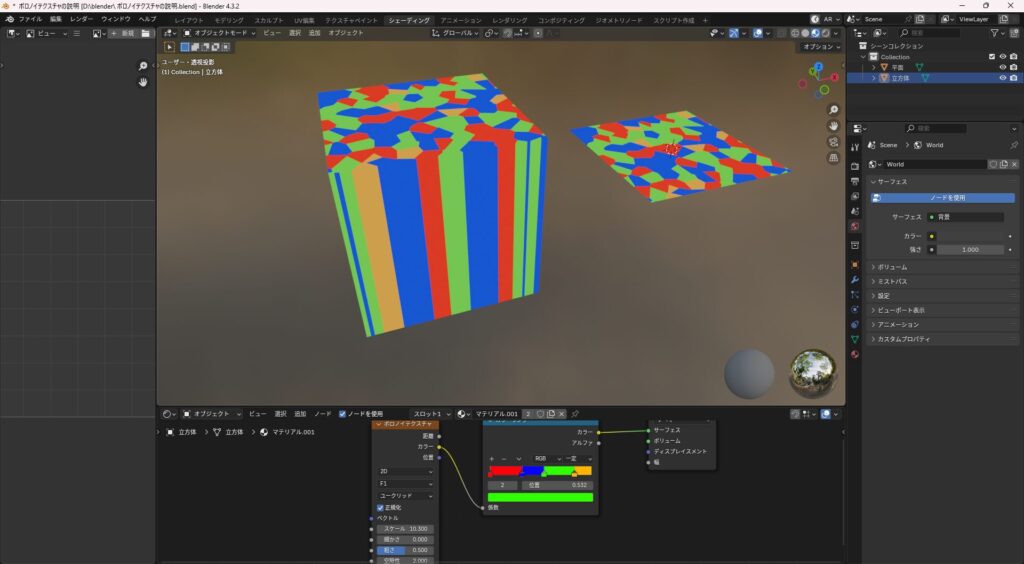
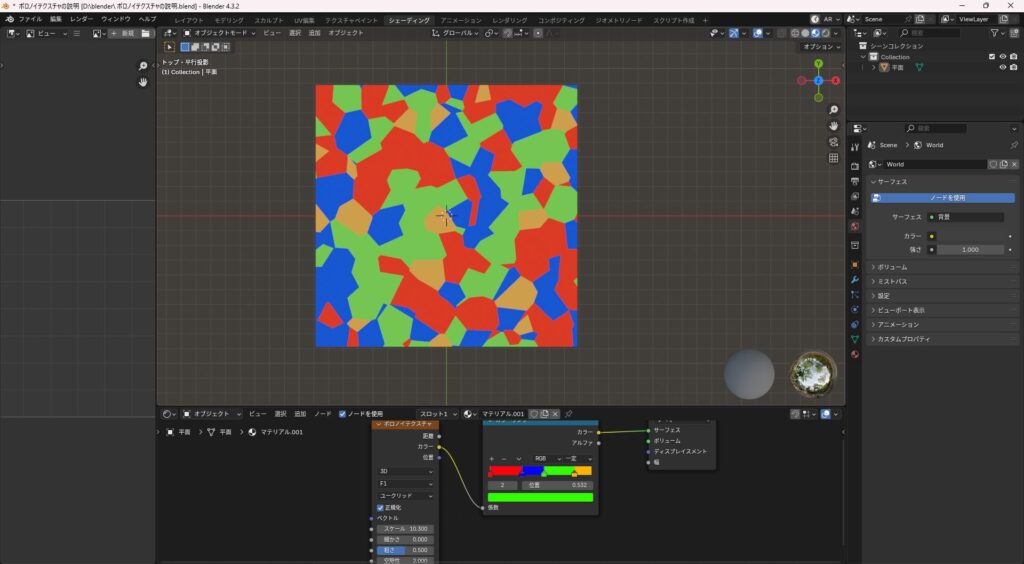
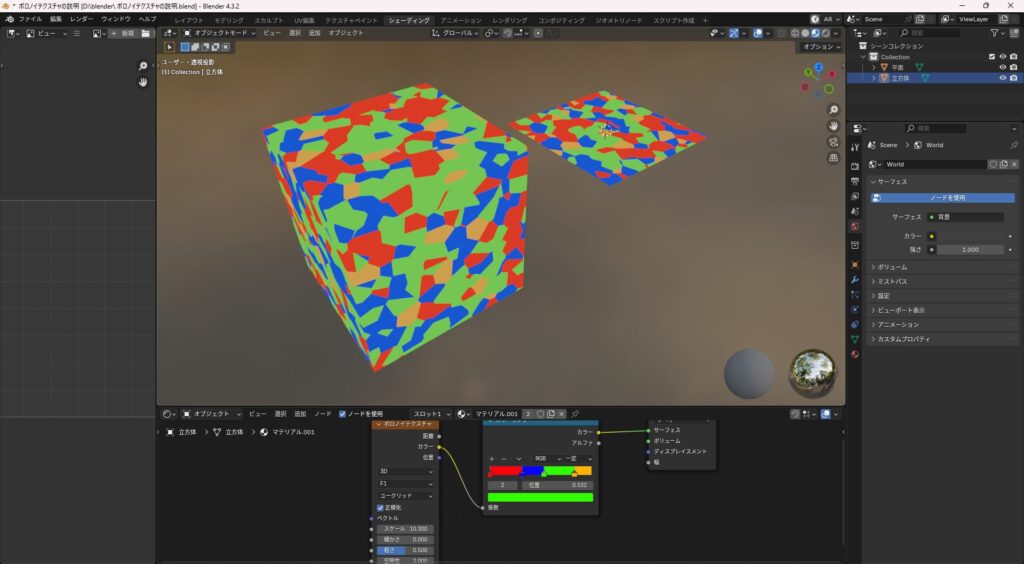
3D(3次元)
- X・Y・Zの立体空間全体に模様が広がる
- オブジェクト内部まで続く模様を作れる
- 切断面やボリューム感を出したい時に便利
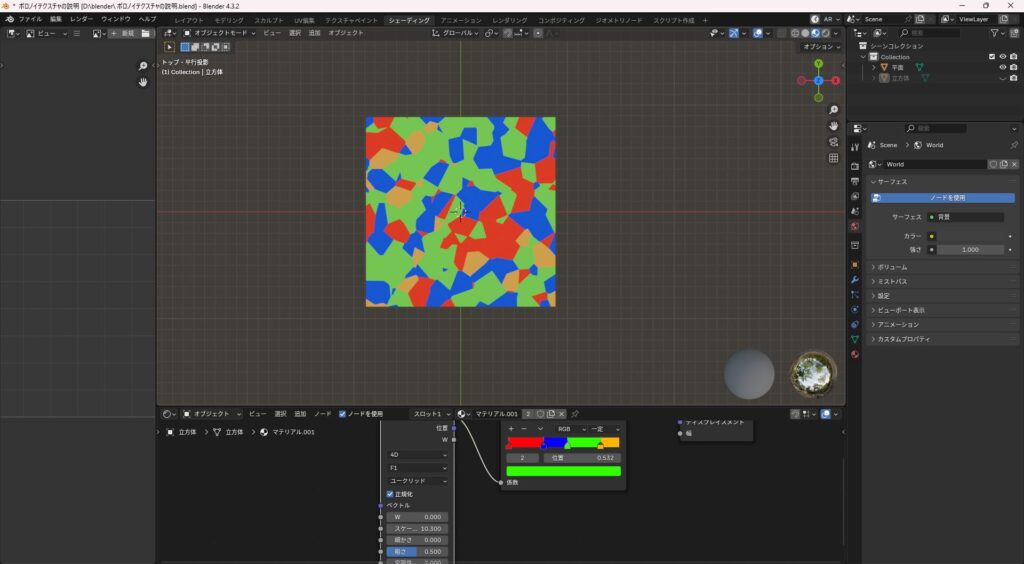
4D(4次元)
- 通常の3次元に「W軸(時間や追加の変数)」をプラス
- 時間で模様が変化するアニメーション表現が可能
- 水面の揺れやノイズの変化、幻想的なエフェクトにも使える
次元は高くなるほどレンダリングに時間がかかります。
レンダリング時間を短縮するなら、なるべく低い次元で表現することをお勧めします。
実際に使う場合
ここまでボロノイテクスチャの概要などをやってきました。
では、実際にボロノイテクスチャを使用した例、使い方を見ていきましょう!
色について
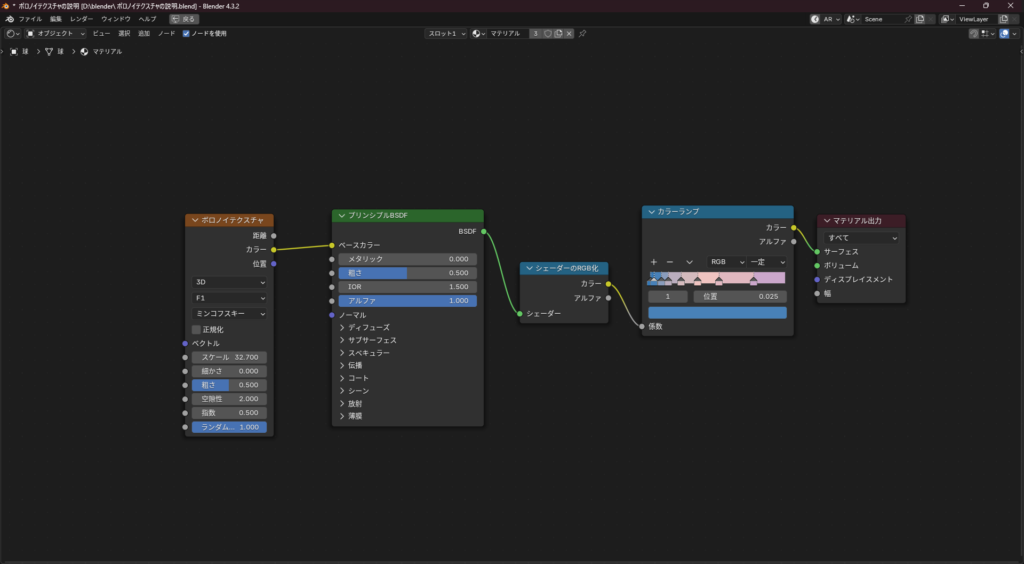

このノードはEeveeのみですが、アニメ調に色を分けるノードの最初にボロノイテクスチャをくっつけることでランダム性が追加されます。
ノードのつなぎ方によって境界線の形なども変更できます。
形について
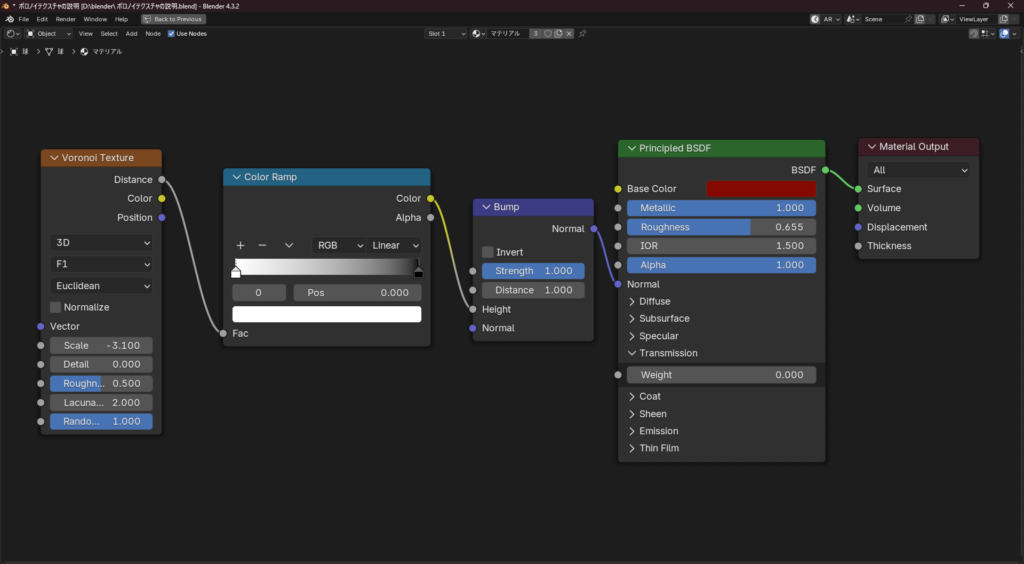

カラーランプを使い、白と黒を反転させることでボロノイの中央を膨らませることができます。これはベリー類などのモデリングなどに使えます。
質感について
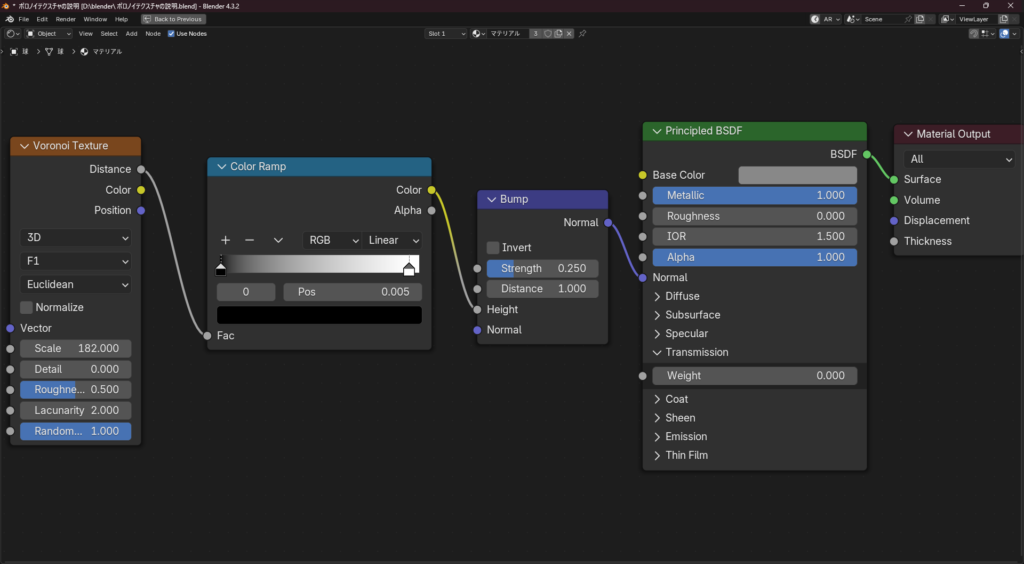

ボロノイテクスチャのスケールの値を大きくすることで細かいノイズテクスチャのようにできます。距離の算出方法を変更することで質感を変更することができます。
まとめ
ボロノイテクスチャは、一見すると難しそうな数式やパラメーターが並ぶノードですが、その仕組みを知れば「模様の生成原理」がなんとなく分かるようになります。
ユークリッド・マンハッタン・チェビシェフ・ミンコフスキーといった距離の違い、F1・F2による見た目の変化、そして次元設定による用途の幅広さなど、理解を深めることで応用力が大きく広がります。
自然な質感、手描き風アニメ調、リアルな石や皮膚のパターンまで、アイディア次第でどんな表現にも活かせるテクスチャです。
まずは簡単なノード構成から始めて、色・形・質感といった視点でじっくり試してみてください!
Blenderのノードは1つのノードで完結させるというより、複数のノードを組み合わせて探していくパズル的な要素があるので様々なノードに触れて感覚を養ってみてはいかがでしょうか?




コメント